dp/common/transformations

Reference Frames

Many reference frames are used throughout. This folder contains all helper functions needed to transform between them. Generally this is done by generating a rotation matrix and multiplying.

Name	[x, y, z]	Units	Notes
Geodetic	[Latitude, Longitude, Altitude]	geodetic coordinates	Sometimes used as [lon, lat, alt], avoid this frame.
ECEF	[x, y, z]	meters	We use ITRF14 (IGS14), NOT NAD83. This is the global Mesh3D frame.
NED	[North, East, Down]	meters	Relative to earth's surface, useful for visualizing.
Device	[Forward, Right, Down]	meters	This is the Mesh3D local frame. Relative to camera, not imu.
Calibrated	[Forward, Right, Down]	meters	This is the frame the model outputs are in. More details below.
Car	[Forward, Right, Down]	meters	This is useful for estimating position of points on the road. More details below.
View	[Right, Down, Forward]	meters	Like device frame, but according to camera conventions.
Camera	[u, v, focal]	pixels	Like view frame, but 2d on the camera image.
Normalized Camera	[u / focal, v / focal, 1]	/
Model	[u, v, focal]	pixels	The sampled rectangle of the full camera frame the model uses.
Normalized Model	[u / focal, v / focal, 1]	/

Orientation Conventions

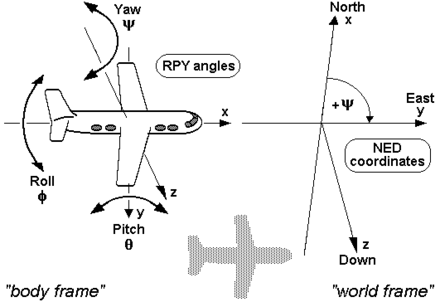
Quaternions, rotation matrices and euler angles are three equivalent representations of orientation and all three are used throughout the code base.

For euler angles the preferred convention is [roll, pitch, yaw] which corresponds to rotations around the [x, y, z] axes. All euler angles should always be in radians or radians/s unless for plotting or display purposes. For quaternions the hamilton notations is preferred which is [q_w, q_x, q_y, q_z]. All quaternions should always be normalized with a strictly positive q_w. These quaternions are a unique representation of orientation whereas euler angles or rotation matrices are not.

To rotate from one frame into another with euler angles the convention is to rotate around roll, then pitch and then yaw, while rotating around the rotated axes, not the original axes.

Car frame

Device frame is aligned with the road-facing camera used by openpilot. However, when controlling the vehicle it is helpful to think in a reference frame aligned with the vehicle. These two reference frames can be different.

The orientation of car frame is defined to be aligned with the car's direction of travel and the road plane when the vehicle is driving on a flat road and not turning. The origin of car frame is defined to be directly below device frame (in car frame), such that it is on the road plane. The position and orientation of this frame is not necessarily always aligned with the direction of travel or the road plane due to suspension movements and other effects.

Calibrated frame

It is helpful for openpilot's driving model to take in images that look similar when mounted differently in different cars. To achieve this we "calibrate" the images by transforming it into calibrated frame. Calibrated frame is defined to be aligned with car frame in pitch and yaw, and aligned with device frame in roll. It also has the same origin as device frame.

Example

To transform global Mesh3D positions and orientations (positions_ecef, quats_ecef) into the local frame described by the first position and orientation from Mesh3D one would do:

ecef_from_local = rot_from_quat(quats_ecef[0])
local_from_ecef = ecef_from_local.T
positions_local = np.einsum('ij,kj->ki', local_from_ecef, postions_ecef - positions_ecef[0])
rotations_global = rot_from_quat(quats_ecef)
rotations_local = np.einsum('ij,kjl->kil', local_from_ecef, rotations_global)
eulers_local = euler_from_rot(rotations_local)